Stitch Fix values the input of both human experts and computer algorithms in our styling process. As we’ve pointed out before, this approach has a lot of benefits and so it’s no surprise that more and more technologies (like Tesla’s self-driving cars, Facebook’s chat bot, and Wise.io’s augmented customer service) are also marrying computer and human workforces. Interest has been rising in how to optimize this type of hybrid algorithm. At Stitch Fix we have realized that well-trained humans are just as important for this as well-trained machines.
There are similarities and differences between training humans and computers. In regards to similarity both respond well to repetition and feedback. However, computers don’t care if their feedback is served in a timely fashion while humans need it promptly. Computers also don’t care about the order of their training set, but teaching a child math needs to start with two plus two and not the square root of negative-one. This shows how important it is to consider these differences when training humans and/or computers.
We have honed in on a specific way to teach people that allows us to provide a focused training program with these uniquely human qualities in mind. Our developed approach provides our stylists (human workforce) with tests based on our client purchase history, in which they decide whether or not a client loved something. The questions are purposefully ordered and each response is followed by immediate feedback.

Our approach to question ordering follows learning theory from cognitive science (e.g., Dedre Gentner’s work on progressive alignment) and selects a series of questions that are ordered from easiest to most difficult. The goal is to allow our learners (stylists) to scaffold harder concepts onto easier ones. Given that it can be difficult to figure out which questions are “harder” just by looking at them, we’ve used Item Response Theory (IRT) to make quantitative judgments. IRT has been used for decades in the realms of standardized testing and education, but it has received limited attention in the technology sector. IRT helps develop test items (questions) and can be used to calibrate and understand each question’s difficulty relative to all questions in a set.1
The IRT process begins with a ‘calibration phase’ whereby a series of questions are created (e.g., “would this client love this?”) and given to a sample of participants (workers) to complete in some random order. The result is a set of performance statistics on each question’s difficulty and each participant’s ability.
Once performance data is collected there’s a family of latent or “hidden” variable models available to rank each question. It’s important to select the IRT model specific to the type of questions being calibrated. For example, the Rasch Model is appropriate for questions with binary outcomes (“correct” and “incorrect”, given by questions with possible responses like “yes” and “no”). Suppose you have a binary response, \(y\). The probability of a subject answering an item/question, \(i\), correctly depends on the their ability, \(\beta\), and on the difficulty, \(\theta\) of the test item (client and/or item attributes). Formally we can describe this relationship with the following equation:
\[\begin{align*} \large P(y_{is}\mid\theta_{i}, \beta_{s}) = \frac{1}{1+e^{\beta_{s}-\theta_{i}}} \end{align*}\]which connects the subject’s probability of success and ability with a logistic function, where a higher ability should predict a higher probability of success. This is called the Item Characteristic Curve and a question’s difficulty is the ability value at which the predicted probability of success is 0.5.
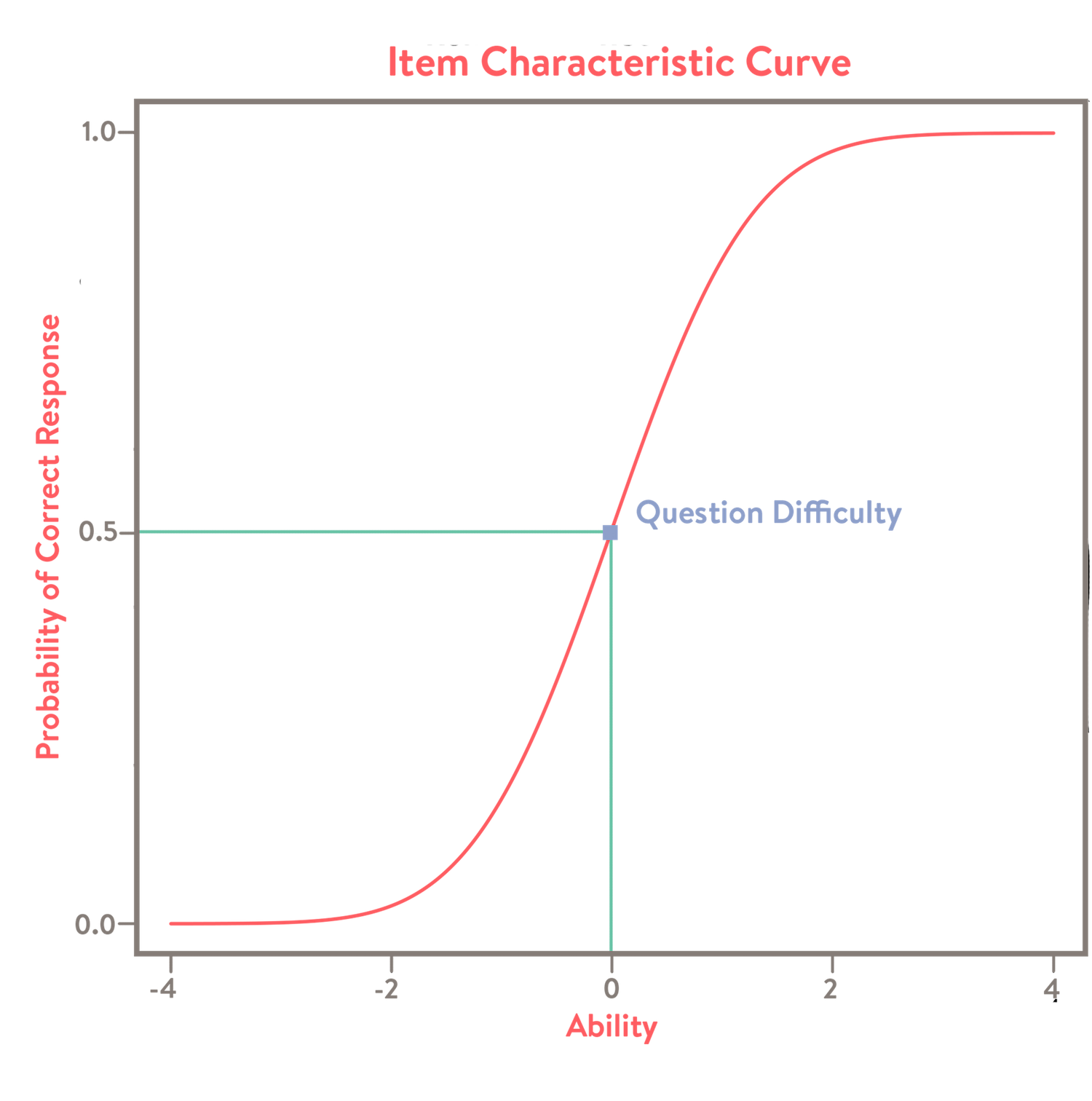
A Rasch Model does such a calculation for every question and will simultaneously estimate each problem’s difficulty and each participant’s ability based on the correctness of each question in a given problem set.
There are a ton of packages that can be used to build these models. Interestingly though, a simple machine learning classifier can be used because the Rasch Model uses a logistic function. Learning item difficulties becomes equivalent to logistic regression with participants and items treated as random effects. Or,
\[\begin{align*} \large correct \sim 0 + (1 \mid subject) + (1\mid item) \end{align*}\]The item intercepts are the relative item difficulties.2 When plotted, they should create a logistic shape showing the more difficult questions with a lower intercept than the easier ones. You should see reasonably small error bars around each intercept, creating something like the shape in this ggplot graph.
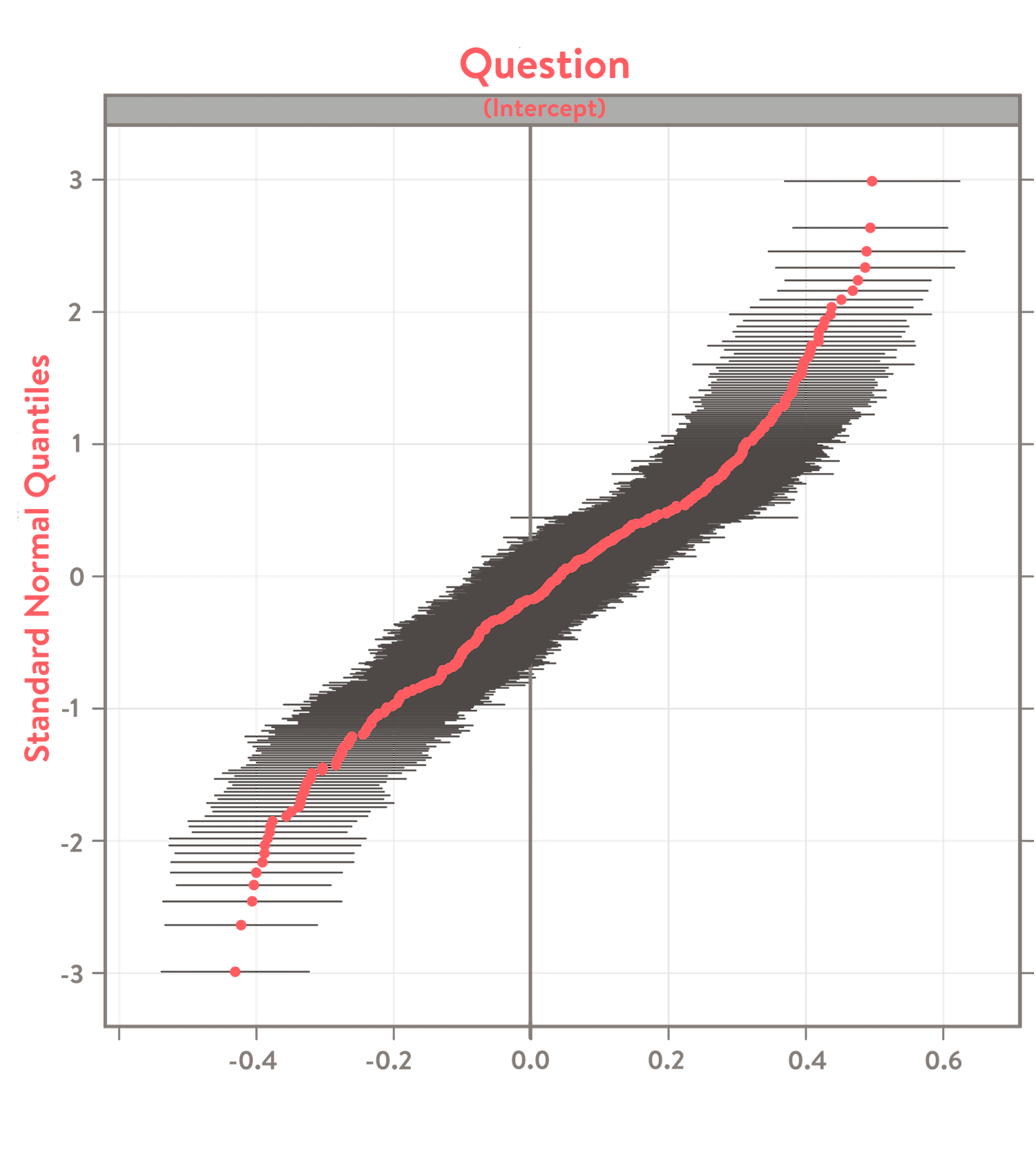
Note that each intercept is a noisy estimate. The error bars give the range of values that the estimated intercept could take. Their sizes and relative shape can help to judge how confident one can be that the questions actually differ. If error bars are large or overlap a lot, then the model is less confident that the questions have different levels of difficulty. Here’s a graphical example of how it would look.
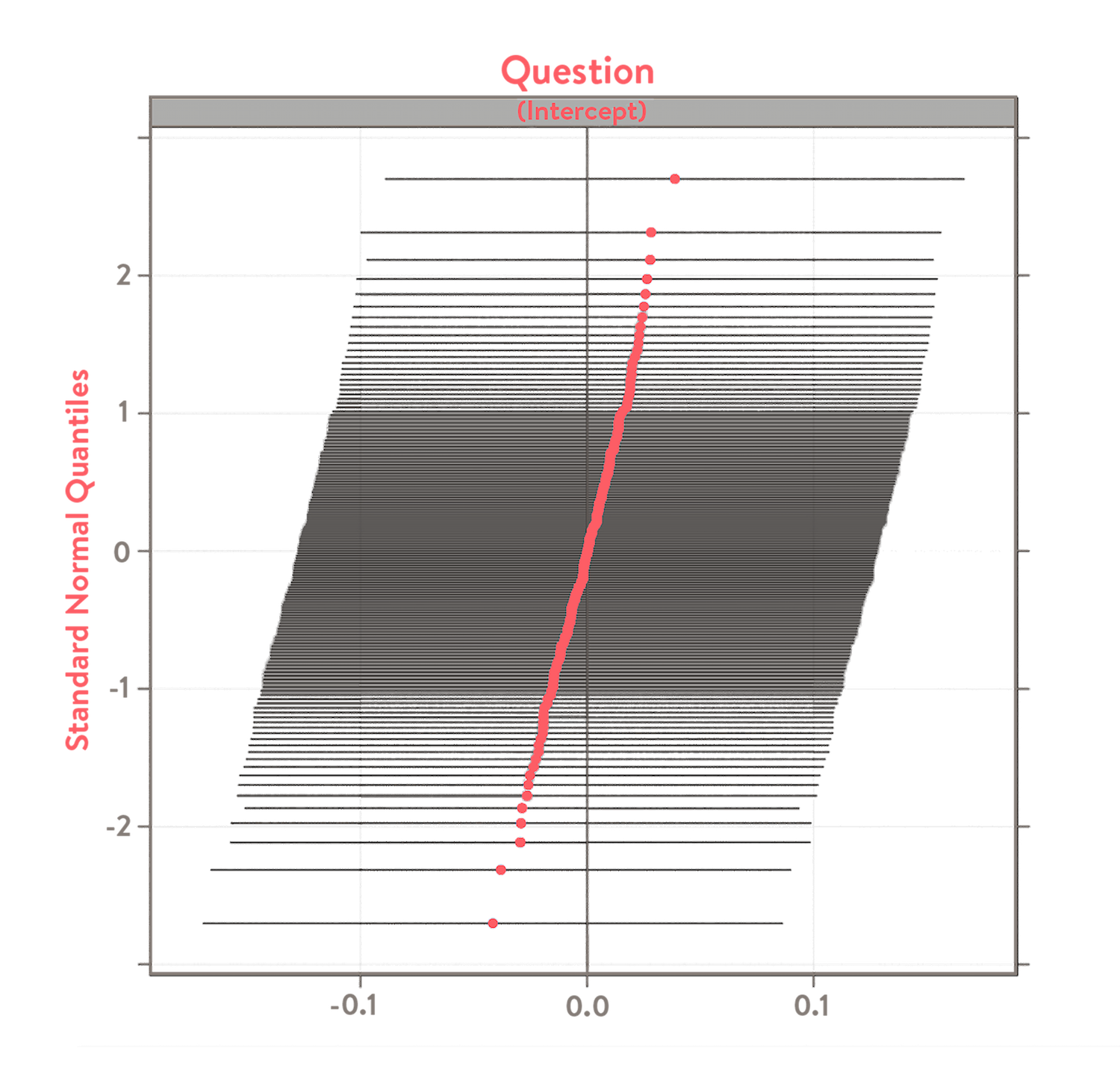
Such a shape implies that the questions might not differ in difficulty. It might then be better to edit the questions and re-calibrate.
If the questions do differ in difficulty as planned, then they can be ordered by “difficulty” such that items with the highest intercepts (i.e., the easiest questions) are shown first and the items with the lowest intercepts (i.e., the hardest questions) are shown last. When this type of ordering is coupled with direct and immediate feedback following the response of each question (e.g., whether each question was answered correctly and why), then the learning environment can bootstrap harder concepts onto easier ones and correct misconceptions along the way.
Ultimately, this IRT-based approach allows us to provide iterative practice and feedback to our human workers. It’s similar to tuning a machine algorithm in that it’s repetitive and targeted at task-related concepts. A key difference is that this training method is also ‘humanized’ in the way that it’s highly curated and organized. Like in the case of any algorithm the overall goal is still to elicit the best predictions possible - no matter what part of the system is making them.
1 For a full review of the IRT, check out the book Item Response Theory by Susan Embretson and Steven Reise. ←
2 Note the 0 in this model is a bit inconsequential, but will center your random effects on 0. This is useful if item difficulty is the primary interest, since relative differences between items will be represented. ←
