We understand that there is a lot going on in the world right now. We’re continuing to publish blog posts in the hope they provide some intellectual stimulation and a sense of connection during these times. See the following for actions that we’re taking regarding racial justice and COVID-19
Multi-Armed Bandits and the Stitch Fix Experimentation Platform
Multi-armed bandits have become a popular alternative to traditional A/B testing for online experimentation at Stitch Fix. We’ve recently decided to extend our experimentation platform to include multi-armed bandits as a first-class feature. This post gives an overview of our experimentation platform architecture, explains some of the theory behind multi-armed bandits, and finally shows how we incorporate them into our platform.
Primer: The Stitch Fix Experimentation Platform
Before getting into the details of multi-armed bandits, you’ll first need to know a little bit about how our experimentation platform works. In our previous post on building a centralized experimentation platform, we explained the #oneway philosophy, and how it makes experimentation both less costly and more impactful. The idea is to have #oneway to run and analyze experiments across the entire business. The same platform is used by front-end engineers, back-end engineers, product managers, and data scientists. And it’s flexible enough to be used for experiments on inventory management and forecasting, warehouse operations, outfit recommendations, marketing, and everything in between. To enable such a wide variety of experiments, we rely on two key concepts: configuration parameters and randomization units.
Configuration-Driven Experiments
A configuration parameter represents whatever is being varied in an experiment. It could be anything from the choice of welcome text on a landing page, to the number of items we display to a stylist when they’re choosing items for a fix, to the value of a hyperparameter for a machine learning model that recommends items on our Shop Your Looks page. These parameters are not just about controlling incremental changes to existing systems. They can also be used to represent huge changes, such as deploying a new backend for our purchase order platform, or an entirely new inventory strategy. In these cases, the parameter values would represent versions of the program or algorithm being tested.
From the platform’s point of view, a configuration parameter is just a name and a set of allowed values. The behavior associated with a value is known only to the client application. For example, in a red/blue button A/B test, the StitchFix.com homepage would register a front_page.button_color configuration parameter, with allowed values “red” and “blue”, and the fraction of traffic that should be allocated to each value. When a visitor comes to the page, a request is sent to the experimentation platform containing the front_page.button_color configuration parameter, along with the visitor_id. The allocation engine handles randomization and serving a value back to the page. In this way the allocation engine can be used as a randomized key-value store by any application that wants to conduct experiments.
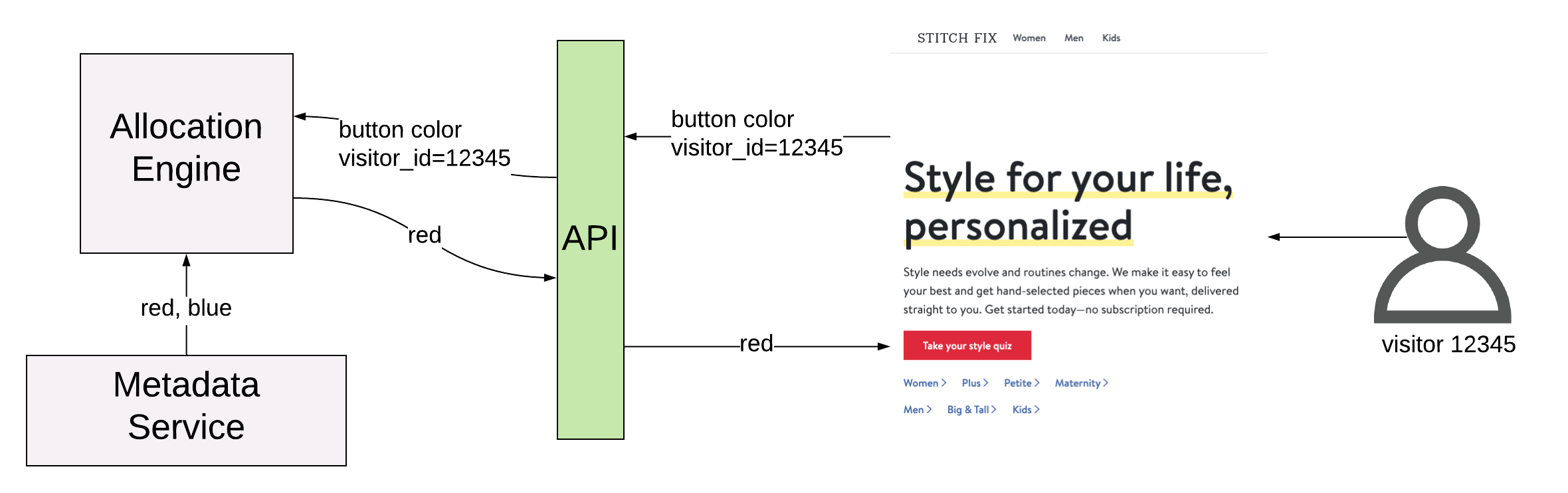
Of course, not all applications will want to randomize on visitor_id. For some experiments it might make sense to randomize on shipment_id or even warehouse_id. To expand the scope of possible experiments, we need another abstraction: the randomization unit.
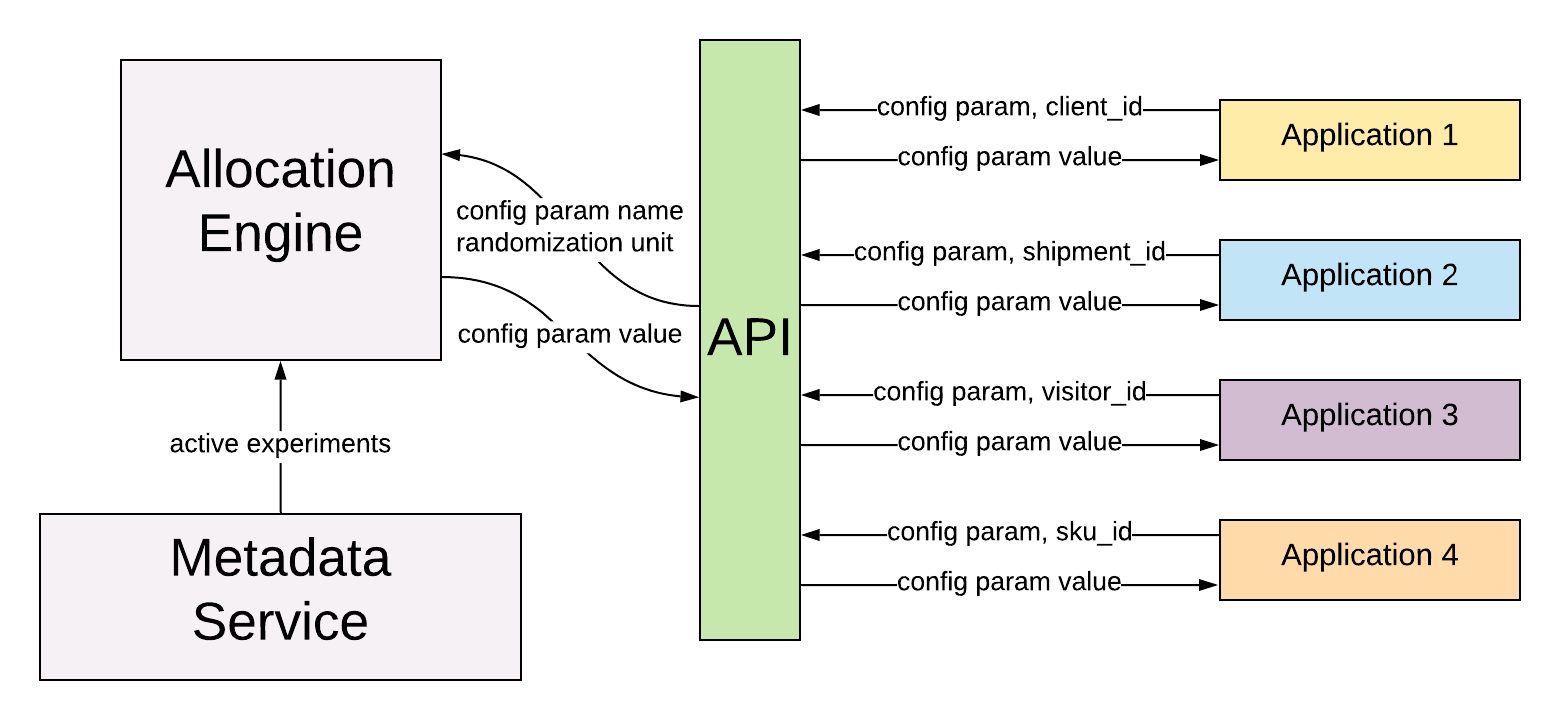
Randomization Units
A randomization unit defines what entity to randomize the experiment on. In the above example of a visitor to the Stitch Fix homepage, the randomization unit was visitor_id. When testing out different versions of the algorithm used to recommend items to stylists, an experiment might randomize on shipment_id or stylist_id. Like with configuration parameters, users can register new randomization units in the platform whenever they need to. An experiment has exactly one randomization unit, but can randomize multiple configuration parameters simultaneously. By mixing and matching randomization units and configuration parameters, our users can create almost any type of experiment they can imagine!
Deterministic Allocations
A key feature of the allocation engine is the ability to perform random allocations deterministically. This guarantees, for example, that if the same visitor visits the same page more than once, they will be allocated to the same experiment cell each time, ensuring a consistent experience. For a given experiment and randomization unit, the allocation engine will reliably return the same cell selection each time. To achieve this without having to store every allocation decision in a database and look them up at allocation time, the choice of cell is determined by a hashing function.
First, each experiment cell is mapped to an exclusive subset of the integers between 0 and 999. Then for each allocation, we generate a pseudo-random number in this range by taking the sha1 hash of the experiment_id and randomization unit, modulo 1000. For example, if the experiment is randomizing on visitor_id, the random number generation function would be:
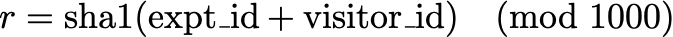
The outcome of this function will be an integer between 0 and 999, and the visitor will be assigned to the corresponding cell. The fraction of allocations assigned to each cell will be proportional to the number of integers to which it is mapped.
Multi-Armed Bandit Experiments
Now that you know a little bit about how we handle A/B tests in our experimentation platform, let’s take a moment to introduce the topic of multi-armed bandits. Like an A/B test, a multi-armed bandit involves randomly allocating traffic to different versions of a web page or algorithmic recommendation, in order to determine which variant results in better outcomes. For A/B tests we usually refer to these different variants as “cells”, but in the context of multi-armed bandits, we refer to them as “arms.” Unlike an A/B test, a multi-armed bandit learns to divert traffic away from poorly-performing arms and towards the better-performing ones. A multi-armed bandit experiment often assigns more observations to the optimal arm more quickly than an A/B test. As a result, the opportunity cost of a multi-armed bandit experiment can be lower than that of an A/B test.
In an A/B test, a fixed proportion of traffic is sent to suboptimal cells for the entire length of the experiment, resulting in relatively high opportunity cost. If your goal is to learn which cell is optimal, while minimizing opportunity cost during the experiment, a multi-armed bandit can be a better choice. This is especially true when the rate of traffic is low, or when the number of cells you want to test is large. In the context of multi-armed bandits, the opportunity cost is referred to as regret, and various algorithms exist to minimize regret while learning which experimental cell has the best outcomes. Of course, this efficiency is not without tradeoffs. In any experiment, there is some chance of drawing the wrong conclusion due to the randomness of statistical sampling. A/B tests allow for straightforward control of these error rates, and computing confidence intervals after an A/B test is also a relatively simple procedure. For multi-armed bandits, it can be much harder to estimate confidence intervals and control error rates.
Bandits can also be used for more than just fixed-term experiments. They can be used as a foundation for long-term optimization. As the performance of different arms changes, the bandit algorithm can change how much traffic is sent to those arms. Poorly-performing arms can even be entirely removed and replaced with new variants. In this way it’s possible to continuously test out new ideas while still making sure that most traffic is sent to the best-performing arms.
In Theory
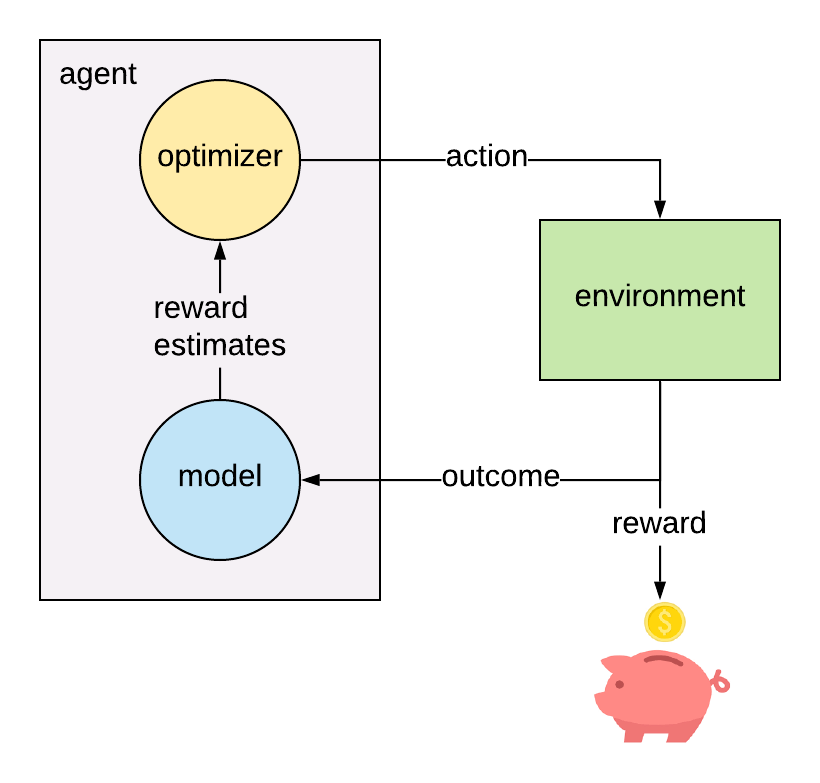
The multi-armed bandit model is a simplified version of reinforcement learning, in which there is an agent interacting with an environment by choosing from a finite set of actions and collecting a non-deterministic reward depending on the action taken. The goal of the agent is to maximize the total collected reward over time.
At discrete time step t, the agent chooses an action \(a_t\) from the set \(A\) of possible actions. This results in observing an outcome \(y_t\), which is mapped to a reward \(r_t\) through a known reward function: \(r_{t} = f(y_{t})\). The outcome corresponding to each action is a random variable \(Y_{a}\), whose distribution is unknown to the agent. Of course, if the agent knew the outcome distributions, the optimal strategy would be to always select the arm with the greatest expected reward: \(a_{t} = \arg\max\limits_{a \in A}(\mu_{a})\), where \(\mu_{a} = E[f(Y_{a})]\). Lacking this knowledge, the agent must instead estimate the expected reward by interacting with the environment and collecting evidence about the outcomes from each action.
It’s important to clarify the distinction between the outcomes \(y_t\) and the rewards \(r_t\). Often, the outcome and reward are actually the same quantity. For example, if the reward you want to maximize is the open rate of a marketing email, then the reward function would be the identity function: \(r_t = f(y_t) = y_t\), where the outcome \(y_t\) is the binary outcome indicating if the email has been opened. But other reward functions can also be useful. For testing out new versions of our match score algorithm, which recommends items for stylists to add to clients’ fixes, our Data Scientists often use lifetime value (LTV) as the reward metric. Of course, it’s not feasible to wait until the LTV can be observed for each client that’s part of the experiment, unless you’re prepared to run a very long experiment. Instead, Data Scientists use an LTV model, which takes into account shorter-term features such as order value and fix feedback to predict the eventual LTV of a client. In this case the outcome \(y_t\) is the vector of inputs to the LTV model resulting from the action \(a_t\), and the pre-trained LTV model is the reward function. In any case, the reward is always a known function of the outcome. The agent estimates the reward for each arm by modeling the outcome of each arm, and then applying the reward function.
The agent must make decisions based on incomplete information, resulting in a dilemma known as the explore vs. exploit problem. Early in the process, reward estimates are highly uncertain, so the agent is compelled to gather evidence about all the available actions, in order to be more certain about which action is likely to produce the highest average reward. The only way to get this evidence is to choose all of the actions multiple times and observe the outcomes. On the other hand, the agent’s goal is to maximize total reward gathered over time, so the agent should avoid choosing actions that are currently predicted to produce less reward. There are a large number of available algorithms that attempt to automatically balance explore vs. exploit at each time step, based on the observed outcomes from actions taken in the past.
A classic example of a regret-minimization technique is the \(\epsilon\)-greedy algorithm. In this algorithm, the agent will usually choose the action with the greatest current estimated mean reward \(\hat{\mu}_a \), but with probability \(\epsilon\) will instead choose a random action from the set \(A\). A small value of \(\epsilon\) means the agent will be doing more exploiting, while a large value of \(\epsilon\) leads to more exploring. The parameter \(\epsilon\) can be fixed for the length of the experiment, or it can be varied over time. Typically one would start with a larger value of \(\epsilon\) and decrease it over time, so the agent will do more exploration in the early stage of an experiment, and more exploitation in the later stages. The performance of this algorithm depends on the choice of \(\epsilon\) and how it is varied over time.
Recently, a number of Data Scientists at Stitch Fix have instead preferred to use Thompson Sampling for their multi-armed bandits. Thompson Sampling has two properties that make it an especially powerful regret-minimization algorithm: convergence and instantaneous self-correction. Convergence means that, given enough time, the algorithm will always end up selecting the optimal arm. This is important because it means that the algorithm won’t end up stuck selecting a suboptimal arm due to early bad luck. Instantaneous self-correction is a more subtle property, but is very important for achieving minimal regret. An algorithm that is instantaneously self-correcting will tend to select an arm more frequently if the current mean reward estimate is an underestimate of the true mean reward, and will select an arm less frequently if the current reward estimate is an overestimate. This means that the algorithm is less likely to be fooled by the randomness of the outcomes and can therefore converge on the optimal arm more quickly than algorithms that aren’t self-correcting. Algorithms that are not instantaneously self-correcting can still be guaranteed to converge, but will converge more slowly than Thompson Sampling.
In a future blog post, we’ll go into detail about how Thompson Sampling works, and share our novel solution for efficient deterministic online Thompson Sampling.
Adding Bandits to the Experimentation Platform
Our goal was to build support for multi-armed bandits into the existing experimentation platform. We wanted to implement a set of standard bandit policies like \(\epsilon\)-greedy and Thompson Sampling, while also supporting Data Scientists who prefer to implement their own policies. The reward models are implemented by the Data Scientists themselves, and plugged in to the allocation engine via a dedicated microservice for each bandit experiment.
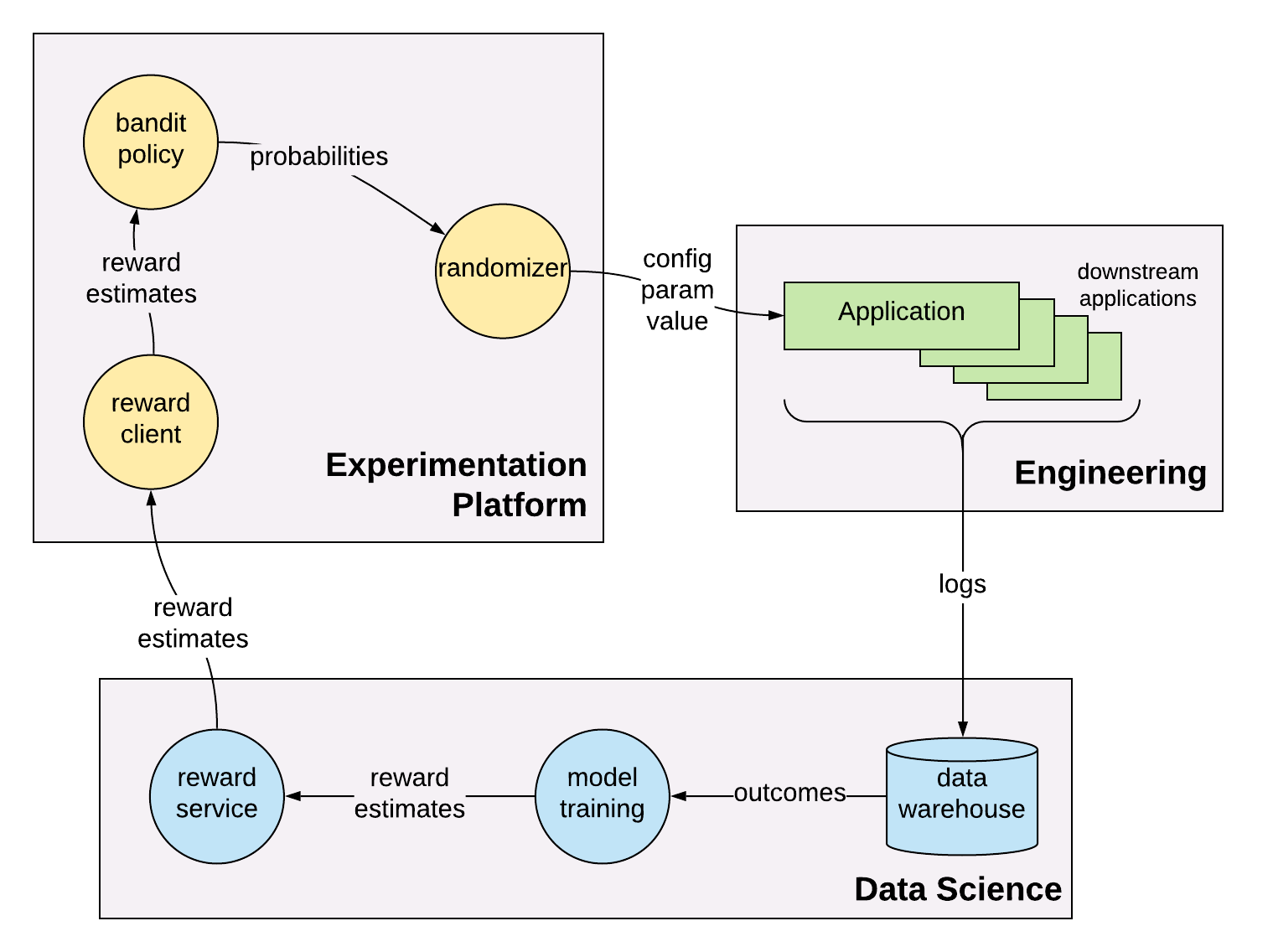
A nice feature of this design is that it requires no changes to the Engineering applications that rely on the allocation engine for configuration parameter values. Those applications don’t even know there’s a new type of experiment - they just continue to consume configuration parameter values and produce logs as if nothing has changed.
Reward Services
Data Scientists are responsible for implementing and updating their own reward models, based on data they can ETL from our data warehouse. Each bandit experiment needs a dedicated microservice that the allocation engine can query for reward estimates at allocation time. At Stitch Fix we have some great tools that help users automate the process of setting up these microservices and keeping their data up-to-date. Data scientists don’t have to worry about things like up-time, latency, and fallbacks. They just have to provide a Python function that returns the reward model estimates, and our “Model Envelope” tool (the new model deployment and tracking system we’re developing) takes care of the rest. Data Scientists can then use our workflow execution scheduler to automate their batch ETLs and update their reward service with new values every time the ETL runs.
When the allocation engine needs to allocate to a multi-armed bandit experiment, it will request reward estimates from the corresponding rewards service. The reward estimates come in the form of distribution parameters. If the bandit is using an \(\epsilon\)-greedy policy, for example, then the reward service only needs to return a point estimate for each cell’s mean reward. In the case of Thompson Sampling, the reward service would provide the parameters of the posterior distribution for each cell. For a Beta posterior, it would provide the values of \(\alpha\) and \(\beta\) for each cell, and for a Gaussian posterior, the values of \(\mu\) and \(\sigma\).
Bandit Policies
Each bandit policy is implemented as a deterministic function that takes in the set of arm reward estimates and outputs the arm selection probability distribution. These probabilities can then be plugged in to our existing allocation engine, which handles the deterministic random allocation.
A bandit policy must be able to compute arm selection probabilities from the set of reward estimates. For the \(\epsilon\)-greedy algorithm, this is a straightforward calculation. The policy only needs to know a point estimate \(\hat{\mu}\) for each arm. Recall that this algorithm works by selecting a uniformly random arm a fraction \(\epsilon\) of the time, and selects the arm with maximal \(\hat{\mu}\) the rest of the time, with ties broken at random. The probability of selecting arm \(a\) is then:
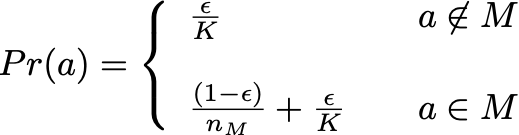
Where \(K\) is the number of arms, \(M\) is the set of arms with maximal \(\hat{\mu}\), and \(n_M\) is the number of cells in \(M\).
Calculating arm selection probabilities for Thompson Sampling is not so easy. Instead of point estimates, Thompson Sampling requires a posterior distribution for the estimated mean reward \(\mu\) for each arm. At each time step, a random sample is drawn from each arm’s distribution, and the arm with the greatest sampled value is chosen. One way to calculate the resulting selection probabilities would be a Monte Carlo method. This would mean repeating the random sampling many times using the same set of distributions, and then counting the fraction of times that each arm would have been selected. This method is far too slow to use for online allocations, so it would have to be done in a pre-compute step. However, this would mean a proliferation of compute jobs, each tightly coupled to a reward microservice. It would also introduce delays between the updates to a reward model and updates to the arm selection probabilities. Additionally, this method becomes computationally expensive for large numbers of arms or small selection probabilities. Wouldn’t it be nice if there was a way to compute Thompson Sampling probabilities that was deterministic, accurate, and efficient enough to be used for online allocations without any pre-compute required? It turns out that there is a way to do it, but you’ll have to wait for my next blog post to find out how :)
We expect that Thompson Sampling and \(\epsilon\)-greedy will cover the majority of use cases, but we don’t want to stop our Data Scientists from using policies that we haven’t implemented yet. For this reason, we added a “proportional” policy, which simply sets each arm’s probability to its estimated mean reward \(\hat{\mu}\), normalized such that the sum of probabilities over all arms is equal to one. If a Data Scientist wanted to implement their own policy, they could configure their reward service to return probabilities instead of reward distribution parameters, and choose the proportional policy to have the allocation engine use their values directly.
Contextual Bandits
So far in this discussion, the agent only knows about the available actions and the observed outcomes for each action in the past. But the agent might be able to do better by making use of additional information about the environment when choosing actions. This additional information is known as context. Generally, context is both environment- and arm-dependent. For example, if the agent was deciding which banner image to show a client when they visit StitchFix.com, the agent might want to take into account the client’s style or brand preferences. In this case, the agent’s reward estimates would depend on both the arm and the context. This more sophisticated model is known as a “contextual bandit”. We have left out the details in this post, but our platform is also built to support contextual bandits.
Conclusion
The experimentation platform at Stitch Fix now supports multi-armed bandit experiments as a first-class feature alongside A/B tests. This gives our Data Scientists a new tool for experimentation, which can provide more efficient optimization than standard A/B tests in some circumstances, and a more flexible method for long-term optimization. Our implementation provides two standardized bandit policies, and an option for users to supply their own. Users are responsible for developing, deploying, and updating their own reward models. The Platform team provides all the tools that Data Scientsts need to build and schedule ETLs for training their models, and for turning a Python model into a microservice. Check back soon for the next Multi-armed Bandit post, where I’ll do a deep dive into a new method for online computation of Thompson Sampling probabilities.
