
A thought experiment: squirrels
Suppose a group of squirrels is considering two possible strategies to survive a harsh winter: either (A) gorge themselves on acorns in the fall and try to make it through the winter on whatever they can find, or (B) bury some acorns in the fall which will then be ready to be dug up in the winter.
Having read a bit about data science, they might choose to A/B test these strategies, randomizing squirrels into two groups. Of course, if the squirrels are sharing the same part of the woods, we can immediately see which group will have a better chance of remaining well fed until springtime — the squirrels of group A with their “greedy” strategy (always optimizing instantaneous rate of calorie consumption) get to stuff themselves all autumn long without setting aside any nuts for the future and continue the eating through the winter by digging up the nuts from their thrifty buddies in group B who have saved acorns throughout the forest floor 1. Group B has a strategy that actually might be superior if it were rolled out to all squirrels, but if they share the same region as group A, their sacrificing some feasting in the fall won’t lead them to be any better off in the winter.
In contrast, if the two experimental groups were placed in separate forests, they would get a better measure of what it would be like to roll out a strategy for all squirrels. Maybe strategy B — saving some acorns for later — is better for squirreldom than greedy strategy A, and maybe not; but the only way an A/B test could possibly reveal B as the winner is if the two groups are not competing for the same underlying resource. Thus, the randomized assignment of squirrels to the two strategies is not good enough; we also have to ensure resources of the two groups are independent.
The importance of getting experiments right
For squirrels, storing acorns is an arduous task. Likewise, creating a new feature or algorithm, setting up a test, and running an experiment is often equally hard work. While it’s not a life-or-death situation for most data scientists, we are still motivated to ensure that our results are correct and that we make optimal business decisions.
Beyond a particular experiment, a data-driven culture requires buy-in across the wider organization, and, by arriving at demonstrably correct decisions, we maintain organizational trust. To this end it’s very important that we identify ways that experiment results can be incorrect in that they don’t indicate what will happen when a change is rolled out fully.
One way that experiments can produce erroneous results is when experimental units are not independent, e.g. due to resource constraints, or a network structure. We explore those problems in this blog post, and discuss in particular how we at Stitch Fix have built a solution based on our own unique situation, which we call the virtual warehouse.
Experimentation and resource constraints
The basics of an experiment
Suppose there are two variants, let’s call them variant A and B, of an experience (a website layout, an algorithm, etc) and we wish to know which one performs best according to some metric we care about (conversion, revenue, client feedback). To that end, we would like to estimate the values of the metric in the case we roll out variant A and when we roll out B. Then we could compare the two and make a decision about which variant to use. The standard A/B testing approach would be to assign half the experimental units (such as users) to variant A and the other half to variant B. When the experimental units are independent, we can estimate the relevant metric on the two groups to compare and finally make a decision.
One of the central assumptions that underlies this approach to making decisions is that the outcomes we observe during the experiment accurately reflect what would happen when either cell is rolled out to all users.
However, different business models and companies face unique challenges for which the above assumption breaks down, because naive randomization does not accurately reflect what would happen if one of the variants is fully adopted. Let’s discuss a few contemporary examples
Network structure
Network structure is a well studied example of when issues arise. The classic example is testing a video chat feature in a social network. If we naively randomize users into “access” and “no access” groups then we will have awkward situations where you have access to video chat but the friend with whom you want to chat does not. One solution to this problem is to find dense clusters in the network and randomize the clusters. In this way, it’s likely that either all friends have access to video, or none of the friends do [1, 2, 3].
Two sided markets
Another set of issues arise in two-sided markets, such as ride-sharing and short-term rentals. Consider an experiment on one side of the market — in this case, one variant of the experiment may affect the other variant through its effects on the other side of the market. To make this a bit more concrete, suppose that the intervention favors the most profitable matches; then the treatment cell may gobble up all of those matches quickly, leaving the control cell to deal with less profitable matches. This might make the treatment cell look really good when compared to the control, but once it is fully rolled out it has to compete with itself rather than the control cell and the gains could vanish. To deal with this issue, companies such as Lyft and Uber have proposed crossover experiments: rather than randomly assigning units to variant A or B for a fixed amount of time, all units are assigned to one variant for some amount of time, and then we crossover to assigning all units to the other variant. This process can be repeated multiple times [4, 5, 6, 7].
Of course, depending on the time-effects on the system, there may still be some interference between the two variants in crossover effects, as it takes a bit of time for the system to reset to its equilibrium under the new variant. To combat this effect, one could ignore data right after the crossover until the system has settled again.
Resource constraints
Issues arising from resource constraints are closely related to those in two-sided markets; the resource constraint ties the two experimental variants together just like the other side of a two-sided market does. In our case, the resource constraint is inventory, though other constraints are also possible, such as monetary ones. To make it more clear: if we decide to add a piece of clothing to a shipment of one client, say under experimental variant A, that particular item is no longer available for future clients, both in variants A and B: whether this is consequential depends on how many other similar items we have in inventory. That it impacts other clients in condition A adds a dependency between observations but this is not the primary concern (in fact, we do want to understand the impact of this dependence). The more problematic aspect is that clients in condition B are also affected, but these should really be independent from those in variant A. That is, we face exactly the same problem in a single warehouse as the squirrels do in a single forest. Building a second warehouse next to our existing one is rather expensive, and geographical differences make it difficult to compare across different warehouses we operate.
In our case, a crossover design does not work because the effects of selecting an item are not short-lived; inventory evolves slowly and thus settling into a new equilibrium after switching to another variant would take a prohibitively long time. So much time that unrelated factors may affect relevant metrics more than the effect from the differences between variants! For example, you can imagine people spending more on clothing in winter because jackets are more expensive than t-shirts.
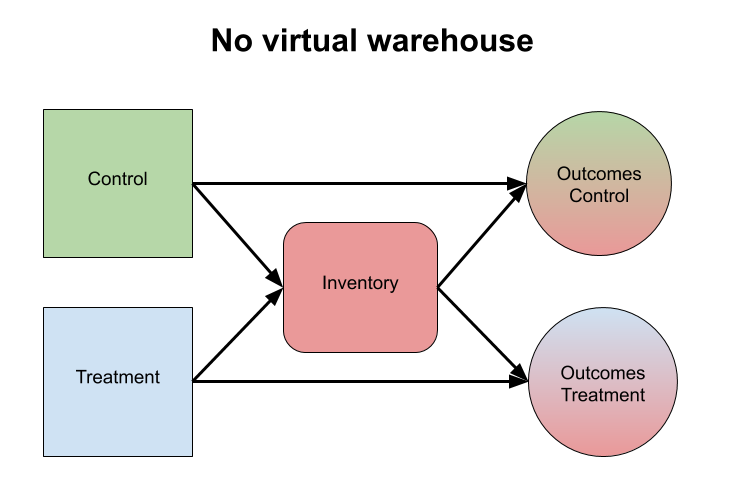
The virtual warehouse
Treatment can affect the outcome directly, or through inventory. Without a virtual warehouse, the latter effect is not contained to the treatment, leading to bias.
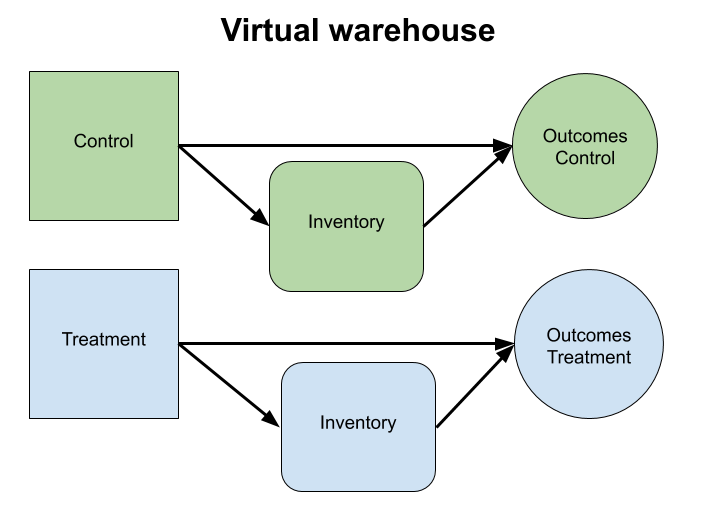
Instead of a cross-over experiment, we use what we call the virtual warehouse to deal with the interference issues from inventory constraints. Recall that we’re considering two variants of an experience — in our case, this might represent versions of a recommendation algorithm. The main idea of the virtual warehouse is simple: we enforce inventory constraints on each variant, cutting the dependence through inventory. In the simplest case, suppose we have 100 identical shirts and two variants to test. Instead of allowing each variant to access however many shirts it is capable of using, we limit each variant to 50 shirts. Of course, in practice it gets a bit more complicated; during the experiment new merchandise arrives in the warehouse, and inventory can be assigned to clients that are not part of the experiment at all, but that simply adds some accounting complexity. Recall the key property we are aiming for: for each variant, we want to simulate what would happen if it were rolled out across all users, which means we need to ensure the variants do not influence each other.
With the virtual warehouse, both the direct treatment effect, as well as the indirect effect due to changes in the inventory equilibrium, are properly separated between treatment and control.
Beyond accounting, there are other complexities. First of all, by splitting the inventory, we are more susceptible to variance due to the square root law of inventory. Secondly, it’s not immediately clear whether it’s possible to run multiple experiments using virtual warehouses at the same time. These topics are out of scope for this blog post, but it is clear that, just like with network clustering and crossover designs, there are downsides to virtual warehouses. At Stitch Fix we have learned that aiming for perfection is not possible when it comes to experimental design, but we can optimize across trade-offs, and the virtual warehouse is a great mechanism for doing so.
Testing inventory strategies with a Virtual Warehouses
So far, we’ve presented the virtual warehouse as a technique for improving the treatment effect estimates and to make better decisions. However, this is not its only benefit. Instead of changing the “treatment” in the form of personalized ranking or curation algorithms, we can leave the treatment identical but change the underlying inventory.
In other words, so far, we have treated the inventory as a nuisance variable which, if we don’t handle it correctly (via virtual warehouses) can ruin inferences about something else that we actually care about (e.g. the ranking algorithm). But inventory is much more than that! It is crucially important in its own right. Getting our inventory to match our clients’ preferences vs getting it wrong can mean a huge difference in how happy our clients (and our company bank account!) are. Reflecting this importance, we have both a large merchandising organization, and a team of over 30 (of our 130+) data scientists optimizing various aspects of the “inventory side”. And the virtual warehouse can help us figure out how to get our inventory right.
In general, finding optimal strategies to inventory problems is challenging. Without a virtual warehouse, it’s hard, if not impossible, to run standard experiments, pitting one strategy against the other and comparing client outcomes; our ultimate metric. But the virtual warehouse enables us to run experiments by creating different inventory conditions virtually. Similar to the above example with 100 shirts, if we have 100 identical shoes in our warehouse, we could split them 50/50 in the virtual warehouses, but we can also divide these 70 to virtual warehouse A and 30 to virtual warehouse B. For a single model of shoe, this might not seem very compelling, but at a larger scale one can imagine rather interesting experiments. For example, what would the impact be on clients and business metrics if we had twice as many shoes in our inventory? Or what is the right amount (as measured by client metrics) of “fall colors” clothing to have in the inventory during the autumn? Or how would the business perform if we had some “loss leaders” in the inventory? Or should we add more depth of our best styles or more breadth of different styles? For the first time in retail history, we can actually answer these questions causally.
If we run a simple split of our inventory into two variants, however, (i.e., if we run a standard “A/B” test) then neither of the experimental variants matches the overall inventory distribution of the company — one variant is skewed in one direction and the other variant is skewed in the other direction from our overall inventory position. We leave as an exercise for the reader the problem of how to use virtual warehouse technology to enable tests of inventory strategies that include a true Control, so that we can compare not just “skewed-one-way” vs “skewed-the-other-way” but also compare to what we’re actually doing as a company.
We’ll go into more detail on this and other virtual warehouse implementation topics in a future post.
Conclusion
When it comes to experimentation, different business models face unique challenges that require thinking beyond the simple randomized control trial to inform decisions critical to the success of companies. At Stitch Fix, we are no exception. Inventory constraints create an undesirable link between observations under different experimental variations. To deal with this, we use the virtual warehouse to split the inventory virtually across variants of an experiment. Furthermore, virtual warehouses also make it easy for us to test different inventory management strategies empirically.
References
[1] J. Ugander et al. - Graph Cluster Randomization: Network Exposure to Multiple Universes
[2] D. Eckles et al. - Design and analysis of experiments in networks: Reducing bias from interference
[3] S. Taylor and D. Eckles - Randomized experiments to detect and estimate social influence in networks
[4] N. Chamandy - Experimentation in a Ridesharing Marketplace
[6] R. Johari et al. - Experimental design in two-sided platforms: An analysis of bias
[7] Bojinov et al. - Design and Analysis of Switchback Experiments
Footnotes
1↩ For the sake of this toy model, we imagine that squirrels find buried acorns in the winter by some combination of scent and digging randomly (even though recent research indicates that in fact they at least partly remember where they buried them). In other words, when they share the same forest, squirrels in group A have just as much access to the acorns that group-B squirrels buried as those in group B have.
